4 Electromagnetism

4.1 Introduction: Electricity, Magnetism, and Light

Electromagnetism is the science of invisible threads that bind our world: sparks that leap, compasses that turn, and light that carries messages from the stars. Before it became a unified theory, electricity and magnetism were curiosities studied in isolation, each with a history stretching back to antiquity.

4.1.1 Ancient Curiosities

The word electricity traces to the Greek elektron—amber. Around 600 BCE, Thales of Miletus noticed that rubbing amber with fur attracted small objects. Static electricity, though puzzling, was a parlor trick. Similarly, lodestones—naturally magnetized pieces of iron ore—were known in China and Greece. They aligned themselves with Earth’s field, guiding compasses centuries before the physics was understood.

Yet for millennia, electricity and magnetism remained folklore and navigation aids rather than systematic science.

4.1.2 Early Experiments in the Age of Enlightenment

In the 18th century, electricity became spectacle. Benjamin Franklin flew his famous kite in a thunderstorm, demonstrating the kinship between lightning and sparks. He coined the terms positive and negative charge and popularized the idea of charge conservation.

Meanwhile, experiments in Italy revealed links between electricity and biology. Luigi Galvani observed frog legs twitch when touched by metal, proposing “animal electricity.” Alessandro Volta disagreed: he argued the source was chemical, not biological, and in 1800 built the first Voltaic pile, the prototype battery. For the first time, a continuous, controllable source of current existed—ushering in a revolution.

Georg Ohm, in the 1820s, quantified the relationship between current, voltage, and resistance:

Ohm’s law, initially resisted, became a cornerstone of circuit theory. Electricity was transforming from curiosity into quantitative science.

4.1.3 The Mystery of Magnetism

Magnetism, too, advanced. The compass was indispensable to explorers. William Gilbert’s De Magnete (1600) argued that Earth itself is a giant magnet. But magnetism seemed separate from electricity. No one suspected that the two phenomena were related.

That changed in the 19th century.

4.1.4 The Industrial Revolution and the Quest for Power

By the early 1800s, steam engines drove factories and railways, but electrical technologies were emerging. Telegraphy promised instantaneous communication across continents. Scientists asked: could electricity power machines, transmit energy, or illuminate cities? Answering these questions demanded deeper theory.

4.1.5 The Puzzle of Light

Another thread entered the story: light. Isaac Newton had described it as particles; Thomas Young and Augustin Fresnel had shown interference and diffraction, confirming its wave nature. But what kind of wave? Sound requires air, water waves require water—so what medium carried light through empty space? Physicists invoked the luminiferous ether, a hypothetical substance filling the void.

The stage was set for unification. The 19th century would reveal that electricity, magnetism, and light were not separate phenomena but faces of one deeper reality.

Electricity began as rubbed amber, magnetism as lodestones, light as mysterious waves. By the dawn of the 19th century, batteries, circuits, and compasses had transformed them into powerful tools—but still separate ones. The next sections will follow Ørsted, Ampère, Faraday, and Maxwell as they forged unity: electromagnetism.

4.2 Ørsted, Ampère, and the Discovery of Electromagnetism

In the early 19th century, electricity and magnetism were still distinct subjects. Batteries produced steady currents; magnets oriented compasses. No one suspected a hidden unity—until a chance experiment in Copenhagen changed physics forever.

4.2.1 Hans Christian Ørsted and the Accidental Discovery

Hans Christian Ørsted (1777–1851) was a Danish physicist and philosopher. Influenced by Romantic Naturphilosophie, he believed nature was unified: electricity, magnetism, chemistry, and light were interconnected. For years, he sought evidence but found nothing conclusive.

In 1820, during a lecture to students, Ørsted noticed something peculiar. A current-carrying wire caused a nearby compass needle to deflect. Electricity, it seemed, could influence magnetism. This was no trivial detail: it implied that electric currents create magnetic fields.

Ørsted’s discovery spread rapidly across Europe. Within months, physicists and mathematicians rushed to quantify the phenomenon. Among them was André-Marie Ampère, who would build the mathematical foundation of electrodynamics.

4.2.2 Ampère’s Experiments and Law

André-Marie Ampère (1775–1836), a French mathematician and physicist, was fascinated by Ørsted’s report. He realized the key was not static electricity but current. Ampère experimented by placing parallel wires with currents side by side and measuring the forces.

He discovered that two parallel currents attract if they flow in the same direction, repel if opposite. This hinted at a new kind of force—between moving charges, not just static ones.

Ampère derived a quantitative expression. The force per unit length between two long parallel conductors a distance $r$ apart is

where $I_1$ and $I_2$ are the currents. This result is so fundamental that the SI definition of the ampere was historically based on it.

More generally, Ampère formulated his law: the circulation of the magnetic field $\mathbf B$ around a closed loop equals the current enclosed:

This Ampère’s law is one of Maxwell’s four great equations (with later correction for displacement current). In modern vector calculus:

4.2.3 Biot–Savart Law

Simultaneously, Jean-Baptiste Biot and Félix Savart investigated the magnetic field produced by currents. They established the Biot–Savart law, describing the field at point $\mathbf r$ due to a current element $I d\mathbf l$:

Integrating along the wire gives the full magnetic field. The Biot–Savart law is analogous to Coulomb’s law for electricity but with the crucial cross product reflecting magnetism’s inherently rotational nature.

4.2.4 Experimental Legacy

These discoveries were not just academic. They laid the foundation for technologies that would transform society:

• Electromagnets. By coiling wires around iron cores, currents produced strong controllable magnetic fields, enabling telegraphs and motors.
• Measurement standards. Current could be measured via magnetic deflection, linking electricity to magnetism in metrology.
• Mathematical electrodynamics. Ampère’s law provided a unifying principle: currents are sources of magnetic fields.

4.2.5 Philosophical Resonance

Ørsted’s experiment validated his intuition of nature’s unity. Ampère’s mathematics revealed that unity quantitatively. Electricity and magnetism were no longer separate curiosities but deeply intertwined. As the poet Goethe had suggested, “The phenomena of nature are only the letters of a mysterious alphabet.” Ampère and Ørsted had decoded a few words of that alphabet.

4.2.6 Toward Faraday and Maxwell

The story did not end there. In the 1830s, Michael Faraday extended the unity further: not only do currents produce magnetic fields, but changing magnetic fields produce currents. This principle of induction (see §4.3) would lead James Clerk Maxwell to complete the unification, showing that light itself is an electromagnetic wave.

In summary: In 1820, Ørsted’s serendipitous compass needle launched a revolution. Ampère’s systematic work quantified the new interaction: currents generate magnetic fields, and their forces obey precise laws. With the Biot–Savart law and Ampère’s circuital law, electromagnetism acquired its first rigorous equations. What began as a lecture-room curiosity became the foundation of modern electrodynamics.

4.3 Faraday and the Field Concept

If Ørsted and Ampère showed that electricity and magnetism are linked, it was Michael Faraday (1791–1867) who gave that link depth and vision. Faraday’s experiments revealed that electricity could be generated from magnetism, not just the other way around, and his idea of “lines of force” laid the foundation for the modern concept of fields.

4.3.1 Faraday’s Life and Character

Born into poverty in London, Faraday had little formal education. He apprenticed as a bookbinder, reading voraciously the scientific texts he bound. Enthralled, he attended lectures by the great chemist Humphry Davy at the Royal Institution. Faraday’s diligence earned him a position as Davy’s assistant. Despite social barriers, Faraday rose to become one of the most celebrated experimentalists in history.

Faraday was not a mathematician. He confessed, “I have not the smallest pretension to mathematical knowledge.” Yet through intuition, experiment, and imagination, he uncovered laws that Maxwell would later encode in mathematics. Faraday exemplified the experimental spirit: careful observation, ingenious apparatus, relentless curiosity.

4.3.2 Discovery of Electromagnetic Induction

The central question after Ørsted was: if currents create magnetic fields, can magnetism create currents? Faraday answered in 1831 with his discovery of electromagnetic induction.

He wrapped two coils of wire around an iron ring. Connecting one coil to a battery and the other to a galvanometer, he saw the needle deflect—but only when the current was switched on or off. A steady current produced no effect; only a changing magnetic flux induced a current in the second coil.

Faraday concluded: a time-varying magnetic field induces an electromotive force (emf). This was a profound symmetry: electricity generates magnetism, and changing magnetism generates electricity.

4.3.3 Faraday’s Law of Induction

Faraday generalized his experiments into a law:

where $\mathcal{E}$ is the induced emf and $\Phi_B$ is the magnetic flux through a circuit:

The minus sign encodes Lenz’s law: the induced current opposes the change in flux, reflecting energy conservation.

In full vector calculus form (later by Maxwell):

This is Faraday’s law, one of the four Maxwell equations.

4.3.4 Lines of Force and the Field Concept

Faraday lacked the tools of calculus, so he described his discoveries with lines of force. He visualized magnetic and electric effects as lines stretching through space, exerting influence locally. To contemporaries accustomed to “action at a distance,” this was radical. But Faraday insisted that space itself was active: fields were real.

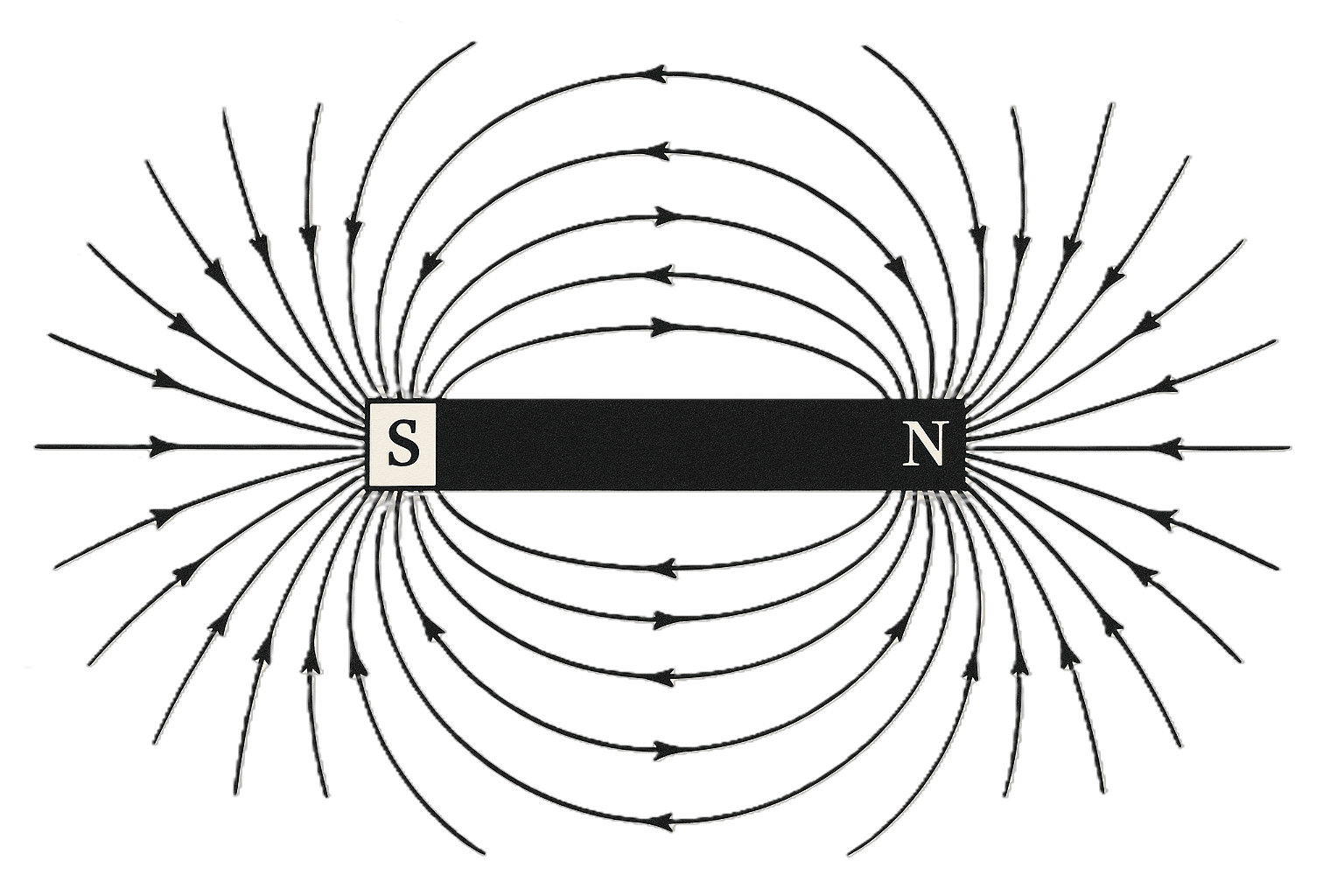
This conceptual leap—fields as physical entities—was as revolutionary as Newton’s gravity. It freed physics from the notion that forces acted instantaneously across empty space. For Faraday, fields were tangible, something one could picture and even sketch.

4.3.5 Experimental Triumphs

Faraday’s laboratory became a theater of discovery:

• Rotating magnet and conductor. He demonstrated that motion between conductor and magnetic field induces currents. This principle underlies electric generators.
• Magneto-optic effect (Faraday effect). He found that a magnetic field rotates the plane of polarized light passing through glass, revealing a link between electromagnetism and optics.
• Electrochemistry. Faraday formulated the laws of electrolysis, introducing terms like electrode, anode, cathode.

These achievements showed his versatility and deep intuition.

4.3.6 Faraday’s Influence on Maxwell

Though Faraday wrote in qualitative language, his field lines captured something profound. James Clerk Maxwell later translated Faraday’s visions into equations. Maxwell acknowledged: “Faraday’s lines of force may be represented mathematically… The whole theory of electromagnetism is the development of this idea.”

Faraday thus bridged experiment and theory. Without his vision, Maxwell’s synthesis might not have emerged.

4.3.7 Technological Impact

Faraday’s induction made practical electricity possible:

• Generators. Mechanical rotation in magnetic fields became the basis of dynamos, powering industry.
• Transformers. Induction between coils allows efficient voltage conversion, essential for power grids.
• Motors. The inverse principle—currents producing motion—completes the cycle.

Faraday’s discoveries underpin nearly every modern technology powered by electricity.

4.3.8 Philosophical Significance

Faraday’s field concept reshaped physics. The idea that space is imbued with fields anticipated both Maxwell’s equations and Einstein’s spacetime. It reflected a new ontology: fields are not mere mathematical conveniences but real actors in nature. As Einstein later remarked, “The greatest change in the axioms of physics, the most fruitful, was Faraday’s concept of the field.”

4.4 Maxwell’s Synthesis: The Equations of the Field

If Faraday provided the experimental vision, it was James Clerk Maxwell (1831–1879) who gave electromagnetism its mathematical soul. Maxwell’s equations unified electricity, magnetism, and optics into a single theory, showing that light itself is an electromagnetic wave. With them, physics gained not only predictive power but a new paradigm: nature is governed by fields obeying differential equations.

4.4.1 Maxwell the Scientist

Born in Edinburgh, Scotland, Maxwell was precociously gifted in mathematics and deeply influenced by Faraday’s writings. Where Faraday drew lines of force, Maxwell translated them into calculus. He worked across physics—color vision, stability of Saturn’s rings, kinetic theory—but his crowning achievement was the synthesis of electromagnetism.

Maxwell was also a philosopher of science. He insisted that equations alone were not enough: one needed models, analogies, and visualization. His blending of intuition and mathematics made him heir to Faraday and prophet of modern field theory.

4.4.2 Maxwell’s Equations in Modern Form

Maxwell consolidated the experimental laws of Coulomb, Ampère, Faraday, and Gauss into four differential equations:

1. Gauss’s law (electric field).
   $\displaystyle \nabla \cdot \boldsymbol{E} = \frac{\rho}{\varepsilon_0}$
   Electric charges $\rho$ are sources of electric field.

2. Gauss’s law (magnetism).
   $\displaystyle \nabla \cdot \boldsymbol{B} = 0$
   No magnetic monopoles exist; field lines are closed loops.

3. Faraday’s law of induction.
   $\displaystyle \nabla \times \boldsymbol{E} = -\,\frac{\partial \boldsymbol{B}}{\partial t}$
   Time-varying magnetic fields induce electric fields.

4. Ampère–Maxwell law.
   $\displaystyle \nabla \times \boldsymbol{B} = \mu_0 \boldsymbol{J} + \mu_0 \varepsilon_0 \,\frac{\partial \boldsymbol{E}}{\partial t}$
   Currents and changing electric fields generate magnetic fields.

The crucial addition is the displacement current term ($\mu_0 \varepsilon_0 \partial \boldsymbol E/\partial t$), invented by Maxwell to preserve charge conservation. Without it, Ampère’s law fails in cases like charging a capacitor. With it, the equations gain consistency and symmetry.

4.4.3 The Wave Equation and the Nature of Light

Combine Faraday’s and Ampère–Maxwell’s laws in free space ($\rho=0$, $\boldsymbol J=0$). Taking the curl of Faraday’s law:

Substitute Ampère–Maxwell:

Using vector identity $\nabla \times (\nabla \times \boldsymbol E) = \nabla(\nabla \cdot \boldsymbol E) - \nabla^2 \boldsymbol E$ and Gauss’s law ($\nabla \cdot \boldsymbol E = 0$ in free space):

This is a wave equation with wave speed

Numerical values of $\mu_0$ and $\varepsilon_0$ gave $c \approx 3.0 \times 10^8 \,\mathrm{m/s}$—the measured speed of light. Thus, light is an electromagnetic wave. This was one of the most stunning theoretical predictions in history: optics was absorbed into electromagnetism.

4.4.4 Field Energy and Poynting Vector

Maxwell also showed that fields carry energy and momentum. The energy density is

and the Poynting vector

represents the energy flux of the electromagnetic field. Light, therefore, is not only vibration but energy in transit. Later, radiation pressure and momentum exchange would be confirmed experimentally.

4.4.5 Symmetry and Unification

Maxwell’s equations are symmetric in $\boldsymbol E$ and $\boldsymbol B$, coupled through time variation. They embody local conservation laws: charge, energy, momentum. They abolished the need for “action at a distance.” Forces arise from local fields, not instantaneous influences.

This symmetry inspired later generalizations. In relativity, Maxwell’s equations acquire elegant tensor form:

with $F^{\mu\nu}$ the electromagnetic field tensor. The unity of electricity and magnetism foreshadowed deeper unifications.

Goal. Show how the four Maxwell equations in 3-vector form,

$$\nabla\!\cdot\!\boldsymbol{E}=\frac{\rho}{\varepsilon_{0}},\quad \nabla\!\times\!\boldsymbol{E}=-\frac{\partial\boldsymbol{B}}{\partial t},\quad \nabla\!\cdot\!\boldsymbol{B}=0,\quad \nabla\!\times\!\boldsymbol{B}=\mu_{0}\boldsymbol{J}+\mu_{0}\varepsilon_{0}\frac{\partial\boldsymbol{E}}{\partial t}.$$

collapse into the covariant pair

$$\partial_{\mu}F^{\mu\nu}=\mu_{0}J^{\nu}, \qquad \partial_{\mu}\tilde F^{\mu\nu}=0,$$

and, if desired, one complex equation by combining $F$ and its dual.

1. Setup: 4D notation & conventions

We work in flat spacetime with metric $\eta_{\mu\nu}=\mathrm{diag}(1,-1,-1,-1)$ and coordinates $x^{\mu}=(ct,x,y,z)$.
We keep SI units explicit, so $c=1/\sqrt{\mu_{0}\varepsilon_{0}}$.

• 4-gradient: $\partial^{\mu}=\left(\tfrac{1}{c}\tfrac{\partial}{\partial t},\,\nabla\right)$
• 4-current: $J^{\mu}=(c\rho,\,\boldsymbol{J})$
• 4-potential: $A^{\mu}=\!\left(\tfrac{\phi}{c},\,\boldsymbol{A}\right)$

Define the field tensor:

Dual:

Matrix form:

And from potentials:

2. Homogeneous equations from geometry

Because $F=dA$, we have

which is

3. Inhomogeneous equations

Equation:

(a) $\nu=0$

(b) $\nu=i$

So

4. One complex equation

Define

Then

which packages both the inhomogeneous and homogeneous equations.

5. Cheatsheet

• Vector form:

• Covariant pair:

• One-liner:

4.4.6 Experimental Confirmation

The German physicist Heinrich Hertz in the 1880s generated and detected radio waves, confirming Maxwell’s prediction. His experiments showed reflection, refraction, and interference identical to light, extending the electromagnetic spectrum. Later, Marconi harnessed them for radio communication, revolutionizing society.

4.4.7 Philosophical and Historical Significance

Maxwell’s unification rivaled Newton’s. Newton had unified celestial and terrestrial mechanics; Maxwell unified electricity, magnetism, and light. In both cases, disparate phenomena fell under a single theoretical umbrella.

Philosophically, Maxwell elevated the field to the central concept of physics. The field is not a mere mathematical tool but a physical reality. Einstein later acknowledged: “The most profound change in the axioms of physics in the 19th century was Maxwell’s introduction of the field.”

4.4.8 Toward Relativity and Beyond

Maxwell’s equations, however, carried a puzzle: they predicted a constant speed of light, independent of the observer. How could this be reconciled with Newtonian relativity? The search for resolution—through Lorentz transformations and Einstein’s special relativity—would form the subject of the next chapter (§5).

4.5 Electromagnetic Radiation

When Maxwell predicted that light is an electromagnetic wave, the claim was breathtaking. It united optics with electricity and magnetism, suggesting that the flicker of a candle and the crackle of a spark were different faces of the same reality. But theory required confirmation. The closing decades of the 19th century would bring that proof, expand the spectrum, and launch technologies that define the modern world.

4.5.1 Wave Properties of Light

Long before Maxwell, light was known to behave as a wave. Thomas Young’s double-slit experiment (1801) showed interference patterns; Augustin Fresnel explained diffraction and polarization. But Maxwell explained what kind of wave: not vibrations of ether, but oscillations of electric and magnetic fields.

Electromagnetic waves are transverse: the electric field $\boldsymbol E$ and magnetic field $\boldsymbol B$ are perpendicular to each other and to the direction of propagation $\mathbf k$. In free space:

The wave carries energy flux given by the Poynting vector:

Thus light is not just illumination but the flow of electromagnetic energy.

4.5.2 Hertz’s Experiments

In the 1880s, Heinrich Hertz tested Maxwell’s theory. Using spark-gap transmitters and resonant loops, he generated radio waves in the laboratory. He observed reflection, refraction, interference, and polarization—all the hallmarks of light. Hertz declared, “I have proved that electromagnetic waves exist in free space.” With that, Maxwell’s prediction was confirmed.

Though Hertz saw no practical use, others quickly did. Guglielmo Marconi adapted the technology for wireless telegraphy, inaugurating the age of radio. Today, every broadcast, cellphone signal, and Wi-Fi connection is a descendant of Hertz’s sparks.

4.5.3 The Electromagnetic Spectrum

Electromagnetic radiation spans a vast spectrum. Wavelength $\lambda$ and frequency $\nu$ obey $c = \lambda \nu$. Different ranges manifest in diverse phenomena:

• Radio waves (km–m): communication, broadcasting, radar.
• Microwaves (cm–mm): cooking, radar, satellite links.
• Infrared (10⁻³–10⁻⁶ m): heat radiation, thermal imaging, astronomy.
• Visible light (400–700 nm): the narrow band our eyes evolved to detect.
• Ultraviolet (10⁻⁸–10⁻⁷ m): sterilization, fluorescence, sunburn.
• X-rays (10⁻¹⁰ m): medical imaging, crystallography.
• Gamma rays (<10⁻¹² m): nuclear transitions, cosmic phenomena.

What unites them all is not their effect on our senses but their origin in oscillating charges and accelerating currents. Antennas, atoms, nuclei—all radiate when charges accelerate.

4.5.4 Antennas and Radiation Mechanisms

Electromagnetic radiation arises whenever charges accelerate. A simple case is the oscillating dipole: charges moving back and forth produce a time-varying current. The radiated field falls off as $1/r$, unlike the static $1/r^2$ Coulomb field, allowing energy to propagate to infinity.

Antennas harness this principle. A half-wavelength dipole resonates with applied currents, efficiently radiating radio waves. Receiving antennas reverse the process, converting incoming radiation into currents. Thus, electromagnetic radiation became not only a natural phenomenon but a tool for communication.

4.5.5 Radiation Pressure and Momentum

Electromagnetic waves carry momentum as well as energy. The pressure exerted on a surface is

where $I$ is intensity. This radiation pressure is tiny in everyday life but crucial in astrophysics: it drives comet tails, balances stellar interiors, and shapes cosmic dust. In the laboratory, it underlies optical tweezers that manipulate single molecules with beams of light.

4.5.6 Electromagnetic Radiation in Nature and Technology

• Astronomy. Almost all information about the universe arrives via electromagnetic radiation. From radio astronomy mapping galaxies to gamma-ray bursts revealing cataclysmic events, the spectrum is our cosmic messenger.
• Medicine. X-rays peer into the body; MRI (though technically nuclear magnetic resonance using radio waves) exploits electromagnetic principles; radiation therapy harnesses high-energy photons.
• Daily life. Light bulbs, lasers, microwaves, Wi-Fi, fiber optics—each a different corner of the spectrum, each indispensable.

4.5.7 Toward Quantum Challenges

By the late 19th century, classical wave theory seemed complete. Yet cracks appeared. Blackbody radiation defied classical predictions; the photoelectric effect revealed particle-like behavior of light. These anomalies would lead to quantum theory (§4.8). Still, the wave view of electromagnetic radiation remains central, forming the backbone of optics, radio, and communication.

4.6 Relativity Emerges

Maxwell’s equations carried a built-in shock: they predict that electromagnetic waves propagate at a speed

a universal constant determined by the properties of free space. Unlike sound or water waves, light seemed not to need a medium. But in the 19th century, physics assumed every wave must have a carrier—an ether filling space. This tension between theory and Newtonian mechanics set the stage for a conceptual revolution.

4.6.1 The Luminiferous Ether

Physicists of the 1800s imagined light waves rippling through a subtle medium, the luminiferous ether. This ether had to be perfectly transparent, extremely rigid to support transverse waves, yet offer no resistance to planets. It was a paradoxical substance, necessary for wave theory but undetectable.

If ether existed, then Earth’s motion through it should produce an “ether wind.” Light traveling along or against this wind would move at different speeds, just as sound travels faster with a breeze. Detecting this effect became an experimental challenge.

4.6.2 The Michelson–Morley Experiment

In 1887, Albert Michelson and Edward Morley performed the definitive test. Their interferometer split a light beam into perpendicular paths, reflected them back, and recombined them. If Earth moved through ether, the interference fringes would shift as the instrument rotated.

The result: no shift. Light’s speed appeared the same in all directions, regardless of Earth’s motion. The experiment, repeated with increasing precision, consistently found no ether wind. The null result was one of the most famous in physics.

4.6.3 Lorentz and FitzGerald Contraction

To rescue ether, some proposed ad hoc fixes. George FitzGerald (1889) and Hendrik Lorentz (1892) suggested that objects contract in the direction of motion by a factor

This “Lorentz–FitzGerald contraction” could explain the null result: the interferometer arms shrank just enough to cancel the effect. Lorentz developed a full mathematical framework, the Lorentz transformations, showing how space and time coordinates must change between moving frames if Maxwell’s equations are to remain form-invariant.

4.6.4 Einstein’s 1905 Revolution

In 1905, a 26-year-old patent clerk named Albert Einstein cut through the ether debate with radical simplicity. He proposed two postulates:

1. Principle of relativity. The laws of physics are the same in all inertial frames.
2. Constancy of the speed of light. Light in vacuum travels at speed $c$, independent of the motion of source or observer.

From these, Einstein derived the full Lorentz transformations—not as a patch for ether, but as the true structure of space and time.

4.6.5 Time Dilation and Length Contraction

Einstein’s relativity predicted strange but testable effects:

• Time dilation. A moving clock ticks slower:

  $$\Delta t = \gamma \Delta t_0, \qquad \gamma = \frac{1}{\sqrt{1-v^2/c^2}}.$$

• Length contraction. A moving rod shrinks along the direction of motion:

  $$L = \frac{L_0}{\gamma}.$$

• Relativity of simultaneity. Events that are simultaneous in one frame may not be simultaneous in another.

These effects, bizarre to Newtonian intuition, have been repeatedly confirmed—by particle lifetimes, GPS satellites, and particle accelerators.

4.6.6 Electromagnetism as the Seed of Relativity

Relativity was not an abstract invention; it was born from electromagnetism. Maxwell’s equations predicted a universal speed of light. Experiments showed no ether drift. Lorentz transformations kept the equations invariant. Einstein elevated these insights to principles of nature.

Electromagnetism thus forced the abandonment of absolute space and time, leading to the fusion of the two into spacetime.

4.6.7 Toward Generalization

Einstein’s 1905 theory, now called special relativity, applied to inertial frames. A decade later, he extended it to accelerated frames and gravitation—general relativity. But the seed of both was Maxwell’s electrodynamics.

4.7 Applications of Electromagnetism

Electromagnetism is not merely a theoretical jewel—it is the foundation of modern civilization. From the light in our homes to the screens in our hands, from medical imaging to interplanetary communication, electromagnetism powers and enables our world. What began with Ørsted’s deflected compass and Faraday’s coils now drives the global economy.

4.7.1 Power Generation: From Faraday’s Disk to the Grid

In 1831, Faraday built a simple generator: a copper disk rotated between the poles of a magnet, producing a steady current. This crude apparatus contained the essential principle: mechanical motion in a magnetic field produces electricity.

Modern generators refine this idea. In power plants—coal, nuclear, hydroelectric, wind—turbines spin coils in magnetic fields, inducing alternating current (AC). Transmission systems rely on transformers, also based on Faraday’s induction, to step voltages up for long-distance transmission and down for safe distribution.

Key concept: AC power and transformers. AC oscillates, enabling induction across stationary coils. This allows efficient voltage conversion and makes large-scale power grids possible. Without transformers, centralized power networks would be impossible.

4.7.2 Electric Motors

The dual of the generator is the motor: electricity producing mechanical motion. When current flows through a coil in a magnetic field, it experiences a torque. This principle powers devices from household fans to industrial robots.

• DC motors. Simple commutators switch current direction to maintain torque.
• AC induction motors. Rotating magnetic fields drive rotor currents; robust and ubiquitous in industry.
• Synchronous motors. Rotor locked in phase with supply frequency; essential for precise timing.

Motors, coupled with generators, create the closed loop of the modern energy economy: mechanical to electrical, electrical back to mechanical.

4.7.3 Communication: From Telegraph to Wi-Fi

Electromagnetism enabled the conquest of distance.

• Telegraph (1830s). Pulses of current along wires transmitted coded messages.
• Telephone (1876). Alexander Graham Bell used varying currents to reproduce speech.
• Radio (1890s). Hertz’s waves, harnessed by Marconi, allowed wireless telegraphy across oceans.
• Electromagnetic spectrum. Today, radio, microwave, and optical communication carry vast streams of data. Fiber-optic cables guide light by total internal reflection; satellites relay microwaves around the globe.

Underlying principle: accelerating charges radiate. Antennas convert currents into electromagnetic waves and back again, bridging space.

4.7.4 Medicine: Imaging and Therapy

Electromagnetism revolutionized medicine, peering into the body and probing its function.

• X-rays. Discovered by Wilhelm Röntgen (1895), high-energy photons reveal bones and tissues.
• MRI (Magnetic Resonance Imaging). Strong magnetic fields align nuclear spins; radio waves perturb them; emitted signals reconstruct images of anatomy with exquisite detail.
• Electrocardiograms (ECG). Measure electrical signals of the heart.
• Radiation therapy. High-energy electromagnetic radiation targets cancer cells.

These techniques exemplify the dual role of electromagnetism: diagnostic and therapeutic, invisible forces illuminating life.

4.7.5 Everyday Technology

Electromagnetism infuses daily life.

• Lighting. From incandescent bulbs to fluorescent tubes to LEDs, all rely on control of electric currents and electromagnetic emission.
• Computing. Transistors switch currents at gigahertz frequencies; electromagnetic pulses shuttle information across chips.
• Wireless devices. Smartphones exchange microwaves with base stations, integrating radio, optics, and electronics.
• Transportation. High-speed trains use magnetic levitation; automobiles depend on motors, sensors, and communication systems.

Every modern device is, at root, an electromagnetic machine.

4.7.6 Astrophysical Applications

Electromagnetism is also the astronomer’s lens. Stars shine by electromagnetic radiation; interstellar clouds emit radio waves; pulsars beam lighthouse signals across the cosmos. Telescopes spanning radio to gamma rays map the universe.

Magnetic fields shape galaxies, launch jets from black holes, and trap plasma in planetary magnetospheres. Without electromagnetism, the universe would be dark and silent.

4.7.7 Engineering Principles: Exergy and Efficiency

Engineering applications hinge on efficiency. Thermodynamics (§3) sets upper bounds; electromagnetism implements them.

• Transmission efficiency. Ohmic losses $I^2 R$ motivate high-voltage lines.
• Electronics. Minimizing power consumption requires reducing resistance, capacitance, and inductive losses.
• Electromagnetic compatibility. Devices must operate without interference, requiring shielding and standards.

Thus, applied electromagnetism is not only about generating fields but managing them for performance.

4.7.8 Electromagnetism and the Digital Age

The digital revolution is electromagnetic at its core. Information is stored as electric charges, transmitted as electromagnetic pulses, displayed as light. Fiber optics carry bits as photons; Wi-Fi radiates them as microwaves; chips process them as electron flows. Claude Shannon’s information theory, formulated in terms of entropy, dovetails with electromagnetic engineering.

In short, the internet is an electromagnetic organism: electrons in wires, photons in glass, waves in air—all governed by Maxwell’s laws.

4.7.9 Philosophical Reflection

When Faraday discovered induction, he could not have foreseen global grids and smartphones. Yet his principle—that changing magnetic flux produces current—underlies them all. The transformation of civilization is, in this sense, the triumph of abstract physics. Electricity and magnetism, once curiosities, became engines of modernity.

Applications of electromagnetism span power, motion, communication, medicine, and computation. Generators light cities, motors drive machines, antennas connect continents, X-rays peer into bodies, and transistors compute. From cosmic signals to digital networks, electromagnetism is the infrastructure of modern life. Maxwell’s equations are not merely abstract—they are the operating manual of civilization.

4.8 Quantum Hints and Field Theory

By the end of the 19th century, electromagnetism seemed complete. Maxwell’s equations unified light, electricity, and magnetism; Hertz had demonstrated radio waves; engineering was thriving with motors, generators, and telegraphs. It looked as though physics had little left but “filling in the details.” Yet the very success of electromagnetism revealed cracks—phenomena that classical theory could not explain. These anomalies would open the door to quantum mechanics and the quantum field theory of electromagnetism: quantum electrodynamics (QED).

4.8.1 Blackbody Radiation and Planck’s Quantum

A blackbody is an ideal object that absorbs all radiation and re-emits energy with a spectrum depending only on temperature. Classical electromagnetism, combined with statistical mechanics, predicted the Rayleigh–Jeans law:

which diverges at high frequencies—an absurdity known as the ultraviolet catastrophe. Experiments, however, showed the spectrum peaks and then decays.

In 1900, Max Planck resolved the paradox by proposing that electromagnetic oscillators exchange energy in discrete quanta:

This radical assumption produced the correct distribution:

Planck had introduced the constant $h$, igniting the quantum era.

4.8.2 Einstein and the Photon: The Photoelectric Effect

In 1905, Albert Einstein explained the photoelectric effect—the emission of electrons from a metal when light shines upon it. Classical theory predicted intensity should control electron energy, with any frequency producing emission given enough time. Instead, experiments showed:

• No electrons ejected below a threshold frequency.
• Above threshold, electron energies depend on frequency, not intensity.
• Intensity affects the number of electrons, not their maximum energy.

Einstein proposed light consists of quanta—photons—each carrying energy $E = h\nu$. An electron absorbs a single photon; if $h\nu$ exceeds the work function $W$, it escapes with kinetic energy:

This particle-like behavior of light shocked physicists and won Einstein the 1921 Nobel Prize.

4.8.3 Compton Scattering and Wave–Particle Duality

In 1923, Arthur Compton observed X-rays scattering off electrons with a frequency shift:

The result matched conservation of energy and momentum if photons are treated as particles with momentum $p = h/\lambda$. Light was undeniably both wave and particle. Maxwell’s continuous fields needed a quantum upgrade.

4.8.4 The Birth of Quantum Electrodynamics

In the 1920s and 1930s, quantum mechanics matured, but reconciling it with electromagnetism required a new framework: quantum field theory. The electromagnetic field was quantized, its excitations identified with photons. Charged particles interact by exchanging photons, virtual or real.

QED was refined in the 1940s by Richard Feynman, Julian Schwinger, and Sin-Itiro Tomonaga, who developed renormalization techniques to tame infinities. Feynman’s diagrams provided intuitive pictures: electron–photon interactions as lines and vertices on paper. QED became the most precise theory in science, predicting quantities like the electron’s magnetic moment to 12 decimal places.

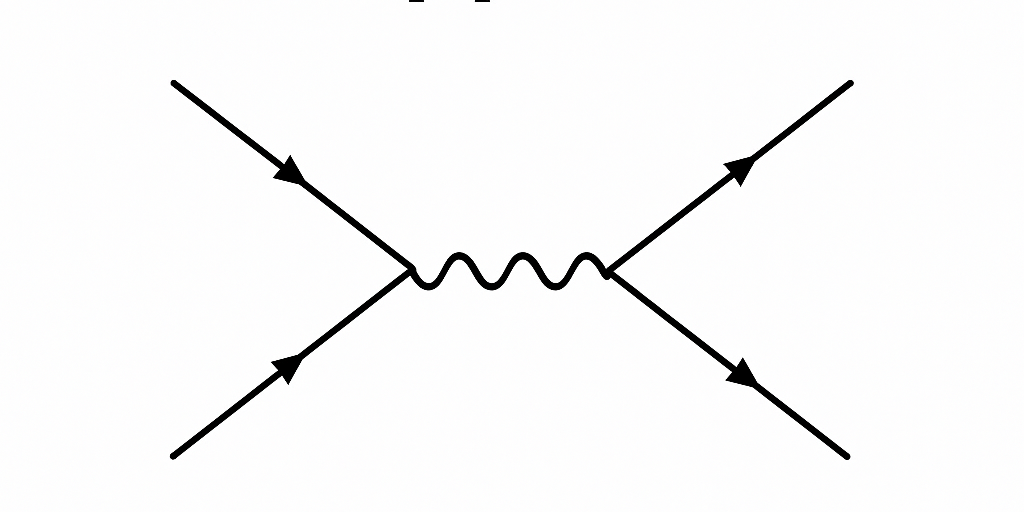
Note. In a Feynman diagram:

• Straight lines with arrows represent fermions (e.g., electrons or positrons).
  • Arrow pointing forward in time: electron.
  • Arrow pointing backward in time: positron.
• Wavy lines represent photons (or, more generally, gauge bosons).
• Vertices are interaction points, where lines meet.
  • In QED, each vertex corresponds to a factor $-ie\gamma^{\mu}$, representing the electron–photon coupling.

4.8.5 Conceptual Shifts

The quantum hints forced deep changes:

• Energy quantization. Light is not infinitely divisible; it comes in discrete photons.
• Wave–particle duality. Light exhibits interference as a wave and scattering as a particle.
• Vacuum fluctuations. Even empty space seethes with virtual photons, producing measurable effects (Casimir force, Lamb shift).

Thus electromagnetism became the first playground of quantum field theory, the prototype for all later gauge theories.

4.8.6 Applications and Modern Impact

Quantum electromagnetism underpins technologies as much as classical does:

• Lasers. Stimulated emission of photons creates coherent light, revolutionizing communication and medicine.
• Semiconductors. Band theory, guided by quantum electrodynamics, drives electronics.
• Quantum optics. Manipulating individual photons enables cryptography and quantum information.
• High-energy physics. QED provides the standard model’s template for electroweak and strong interactions.

4.9 Conclusion: The Unity of Nature

Electromagnetism began as scattered curiosities: amber that attracts straw, lodestones that turn needles, lightning that splits trees, light that dazzles eyes. In the 19th century, these threads were woven together into a single tapestry. The story of electromagnetism is not only about equations; it is about unity—of electricity and magnetism, of light and radiation, of science and technology, of theory and application.

4.9.1 From Ørsted to Maxwell

• Ørsted revealed that currents deflect compass needles, linking electricity to magnetism.
• Ampère quantified the laws of forces between currents.
• Faraday discovered induction, showing that changing magnetic flux produces current, and introduced the vision of fields.
• Maxwell crowned the synthesis with four equations that described electricity, magnetism, and light as manifestations of a single field.

Each step was both experimental and conceptual. What began with sparks and compasses ended with a system of equations capable of predicting the structure of the electromagnetic spectrum and the speed of light itself.

4.9.2 The Concept of the Field

Before electromagnetism, physics assumed action at a distance: forces jump instantaneously across space. Faraday’s “lines of force,” mathematized by Maxwell, changed this worldview. The field became a physical entity, filling space, evolving by local laws. This concept reverberated through all of physics:

• Einstein’s general relativity treats gravity as the curvature of spacetime fields.
• Quantum field theory describes particles as excitations of underlying fields.

The field idea, born in electromagnetism, became the central ontology of modern physics.

4.9.3 The Electromagnetic Spectrum and Technology

From Maxwell’s prediction came Hertz’s verification, Marconi’s radio, lasers, fiber optics, Wi-Fi, MRI, and smartphones. The entire electromagnetic spectrum—from radio to gamma rays—is harnessed for communication, medicine, industry, and exploration. Civilization is, in effect, an electromagnetic enterprise.

Electric power grids distribute energy through induction and transformers. Motors and generators embody Faraday’s principle. Semiconductors and transistors, guided by quantum electrodynamics, run the digital world. From household devices to space telescopes, electromagnetism is the backbone of technology.

4.9.4 Philosophical and Scientific Impact

Electromagnetism redefined the boundaries of physics:

• It demonstrated that apparently distinct forces are aspects of a single reality.
• It established the field as a real physical entity.
• It led directly to relativity, since Maxwell’s equations implied a universal light speed.
• It seeded quantum theory, through anomalies like blackbody radiation and the photoelectric effect.

Thus electromagnetism stands at the crossroads of classical and modern physics, connecting mechanics, relativity, and quantum theory.

4.9.5 Unity as a Guiding Principle

The success of electromagnetism inspired physicists to seek deeper unifications. The electroweak theory unified electromagnetism with the weak nuclear force; grand unified theories aim to combine with the strong force; ultimate hopes target gravity. Each step follows Maxwell’s model: unity hidden beneath diversity, revealed through experiment and mathematics.

4.9.6 The Human Dimension

The story of electromagnetism is also the story of people: Faraday, the poor bookbinder turned experimental genius; Maxwell, the Scottish mathematician who saw fields in equations; Hertz, the experimentalist who made waves visible; engineers and inventors who transformed principles into power grids and radios. It shows how imagination, curiosity, and persistence reshape both science and society.

Electromagnetism unified electricity, magnetism, and light, transformed physics with the concept of the field, and revolutionized technology with motors, generators, and communication. It bridged classical and modern physics, seeding relativity and quantum theory. The unity discovered in sparks and magnets became the foundation of civilization. The legacy of electromagnetism is not only in equations carved on blackboards but in the glow of lamps, the hum of machines, the signals from distant galaxies, and the very photons that let us read these words.